Optical absorption for interband and intersubband transitions
Section author: Takuma Sato
- Input Files:
QWIP_singleQW_GaAs_AlGaAs_nnp.in
QWIP_singleQW_InAs_AlSb_nnp.in
QWIP_Gunapala_JAP_1991_nnp.in
AlGaAs_QW_Frankenberger_Simple_nnp.in
AlGaAs_QW_Frankenberger_Simple_nnp_fast.in
AlGaAs_QW_Frankenberger_Doping_schottky07_nnp.in
AlGaAs_QW_Frankenberger_Doping_schottky07_nnp_fast.in
Contents
In this tutorial we illustrate the optics{ } module to demonstrate what nextnano++ can simulate for optoelectronic devices.
This module performs a detailed calculation to optical absorption phenomena, using 8 (or 6) band
the background physics of this module and how to write the input file, go to Principle and nextnano++ implementation.
the simulation results for intersubband transitions, go to 1D tutorial for intersubband transitions: Quantum well infrared photodetector.
the simulation results for interband transitions, go to 1D tutorial for interband transitions: Frankenberger.
optical absorption in 2D devices, (under construction)
optical absorption in broken-gap structures, (under construction)
This algorithm is implemented based on the following diploma thesis:
Thomas Eißfeller, Linear Optical Response of Semiconductor Nanodevices, Technische Universität München (2008)
For the physics of optical transition in semiconductors and its application, we refer to
Shun L. Chuang, Physics of Optoelectronic Devices (Wiley, 1995)
S.M. Sze & Kwok K. Ng, Physics of Semiconductor Devices (Wiley, 2007)
Principle and nextnano++ implementation
In the k.p analysis of one- (or two-) dimensional structures we have a projection of the Bloch wave vector along translation-invariant directions.
We denote them as
where the Greek indices label the k.p bands and
where Quantum\spinor_composition.
After solving this “Schrödinger” equation, the wave function is integrated over a limited region in
quantum{
region{
kp_8band{
k_integration{
relative_size = $r_quantum # size of k||-space in quantum{ } (relative to the Brillouin zone)
num_points = $N_quantum # number of k|| points where Schrödinger eq. is solved
num_subpoints = $Nsub_quantum # number of points between k|| points where wave functions and eigenvalues are interpolated
force_k0_subspace = # (optional) use the eigenfunctions of the Schrödinger equation at k=0 as the basis for the Schrödinger equation at all k-point (default: no)
}
}
}
}
Note
When force_k0_subspace=yes in quantum{ } or optics{ }, the Schrödinger equations at non-zero k-points are solved in the subspace of the eigenfunctions obtained by the Schrödinger equation at quantum{ }) or the loss in optical spectra is acceptable (optics{ }).
Optical absorption spectrum
When 1) Schrödinger equation is solved with k.p method, 2) optics{ } flag is present and 3) the specifier optics{ } is present under run{ } flag, nextnano++ calculates the absorption spectrum.
optics{
region{
... # see below for details
}
}
run{
quantum{ }
optics{ }
}
The optical absorption accompanied by excitation of charge carriers (state
where the first sum runs over bands that fulfill optics{ occupation_ignore=yes } (default is no), the program assumes
The light polarization
optics{
region{
polarization{ name="TM" re = [1,0,0] } # in 1D simulation, x is the growth direction
polarization{ name="TE" re = [0,1,0] } # complex (circular) polarization is also allowed
refractive_index = # (optional) use alternative value for the refractive index (default: substrate value)
}
}
The core of the optical transition is the optical matrix elements
where the 8
occupation (if
output_occupations=yes) \Optics\occupation_~.dateigenvalue dispersion (if
output_energies=yes) \Optics\energy_disp_~.dattransition intensity (if
output_transitions=yes) Optics\transition_disp_~.datimaginary part of the dielectric function for each transition (if
output_spectra{ output_components yes }) \Optics\imepsilon_~.dattotal imaginary part of the dielectric function \Optics\imepsilon_~.dat
total absorption spectrum \Optics\absorption_~.dat
The following part of the input specifies how much transitions to be taken into account. The setting for k_integration{} is explained in the next section.
optics{
region{
interband = $INTERBAND # yes or no
intraband = $INTRABAND # yes or no
energy_min = $ENERGY_MIN # minimum energy of the absorption spectrum
energy_max = $ENERGY_MAX # maximum energy of the absorption spectrum
energy_resolution = $ENERGY_RESOLUTION # energy grid spacing
k_integration{
relative_size = $r_optics # size of k||-space in optics{ } (relative to the Brillouin zone)
num_points = $N_optics # number of k|| points where transition intensities are computed
num_subpoints = $Nsub_optics # number of points between k|| points where transition intensity is interpolated
force_k0_subspace = # (optional) use the eigenfunctions of the Schrödinger equation at k=0 as the basis for the Schrödinger equation at all k-point (default: no)
}
}
}
Parameters in k_integration{} (for fine tuning)
Parameters in k_integration{} in optics{ } flag (hereafter k_integration{} in quantum{ } flag used for quantum mechanical charge density integration (hereafter
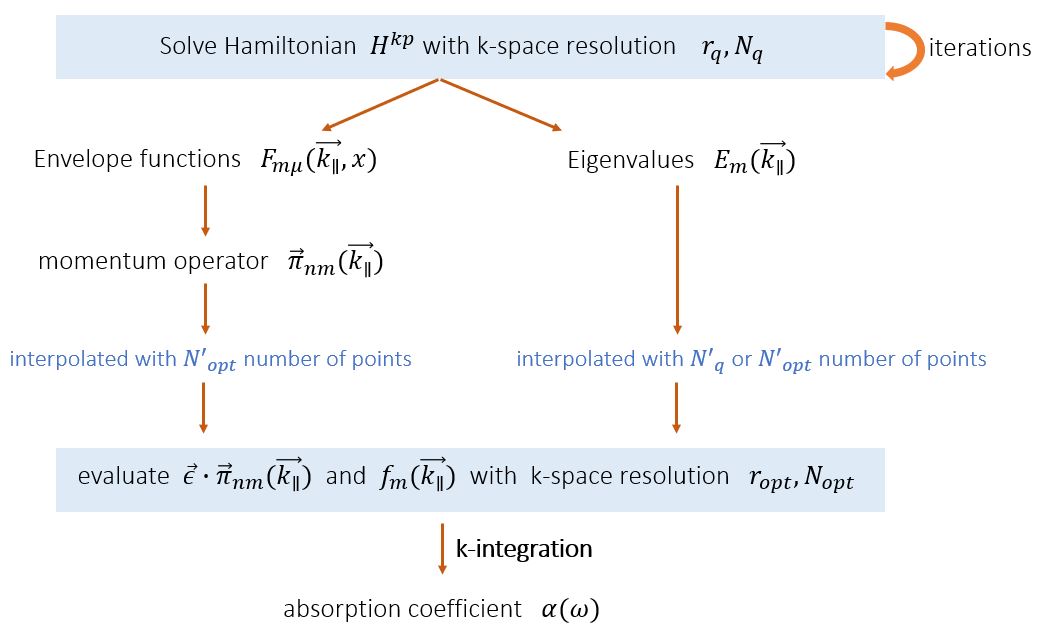
Figure 2.4.311 Calculation algorithm of optical absorption spectrum and its relation to the parameters in k_integration{}. quantum{ } and optics{ }, respectively. To do; the energy dispersion is interpolated with
First we discuss the parameters
In undoped systems, integrating up to
To see the range of occupied states in
\Optics\occupation_~.dat. We recommend checking the box “Show grid” on the left panel in Output tab of nextnanomat (see also Output). This shows the occupation
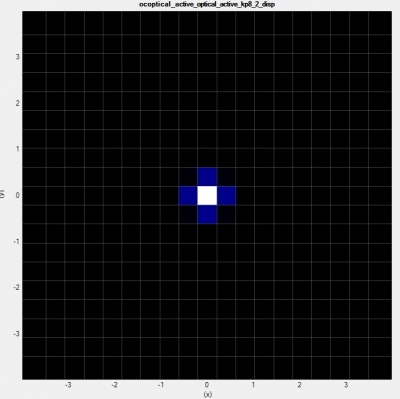
where
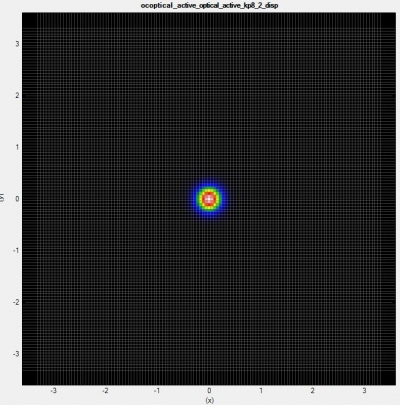
The occupation becomes smooth, but at the same time this significantly increases the number of k points (in 1D simulation, (the number of k points)
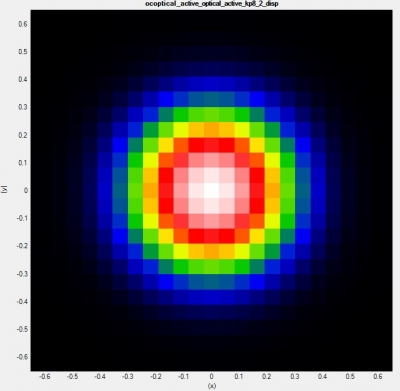
and this should be sufficient for the k||-space integration.
After tuning the parameters

Figure 2.4.312 The effect of the parameter optics{ k_integration{}} on absorption spectrum output \Optics\absorption.
Larger
To do: investigate spin_degeneracy=yes/no and dipole_approximation = yes/no
1D tutorial for intersubband transitions: Quantum well infrared photodetector
In the following we apply the formalism to several devices. As a first example, we model the absorption spectrum of an AlGaAs/GaAs quantum well infrared photodetector (QWIP). The QWIP is based on photoconductivity due to intersubband excitation.
Input files
QWIP_singleQW_GaAs_AlGaAs_nnp.in
QWIP_singleQW_InAs_AlSb_nnp.in
QWIP_Gunapala_JAP_1991_nnp.in
The first example uses the same parameters used in
FIG. 20 in B.F. Levine, J. Appl. Phys. 74 (8), 15 (1993),
while the third example is based on [GunapalaJAP1991]
GaAs/AlGaAs single QW - band structure, eigenstates and absorption
We first illustrate the first example QWIP_singleQW_GaAs_AlGaAs_nnp.in. In this example, we model optical absorption in single quantum well structure. The following input is required for self-consistent quantum-current-Poisson simulation:
quantum{
region{
name = "optical_active"
no_density = no
kp_8band{
num_electrons = $OptNumE
num_holes = $OptNumH
}
}
}
poisson{ }
current{}
run{
strain{ } # strain calculation
current_poisson{ }
quantum_current_poisson{ }
optics{ } # absorption calculation
}
The specifier no_density=no lets the program calculate quantum mechanical charge density (default). Current-Poisson equation takes over this value.
The band structure and wave functions are shown in Figure 2.4.313 and Figure 2.4.314, respectively.
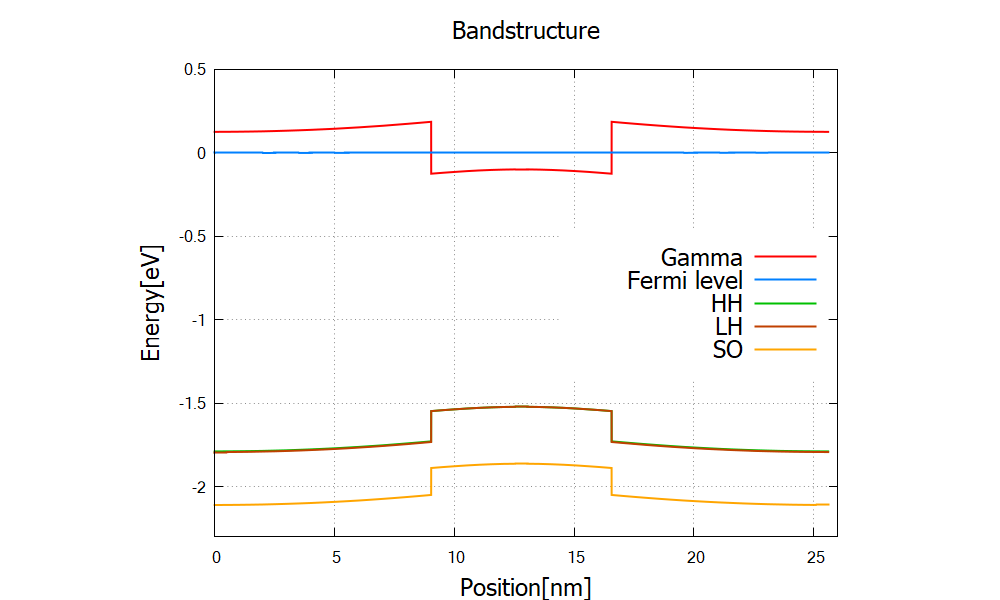
Figure 2.4.313 Single quantum well structure \bandedges.dat. The bias voltage between two contacts is set to 2mV.
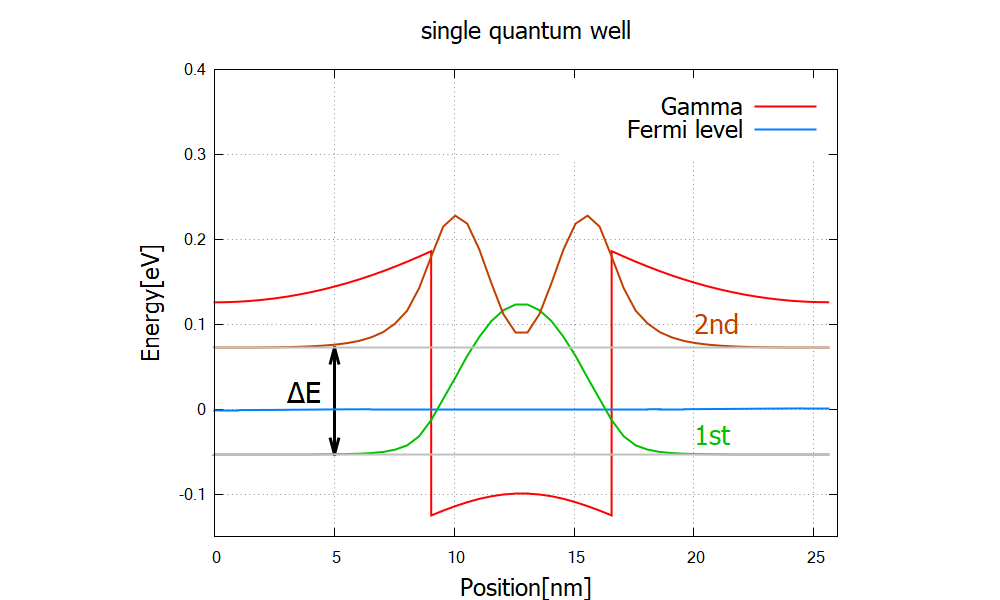
Figure 2.4.314 Probability distribution \Quantum\probabilities_shift_optical_active).
The wave functions here are the solution to the 8-band k.p model.
The energy separation is
The output folder \Optics contains computed absorption spectra.
Let us first check the occupation \Optics\occupation, please mind the autoscale mode of nextnanomat:
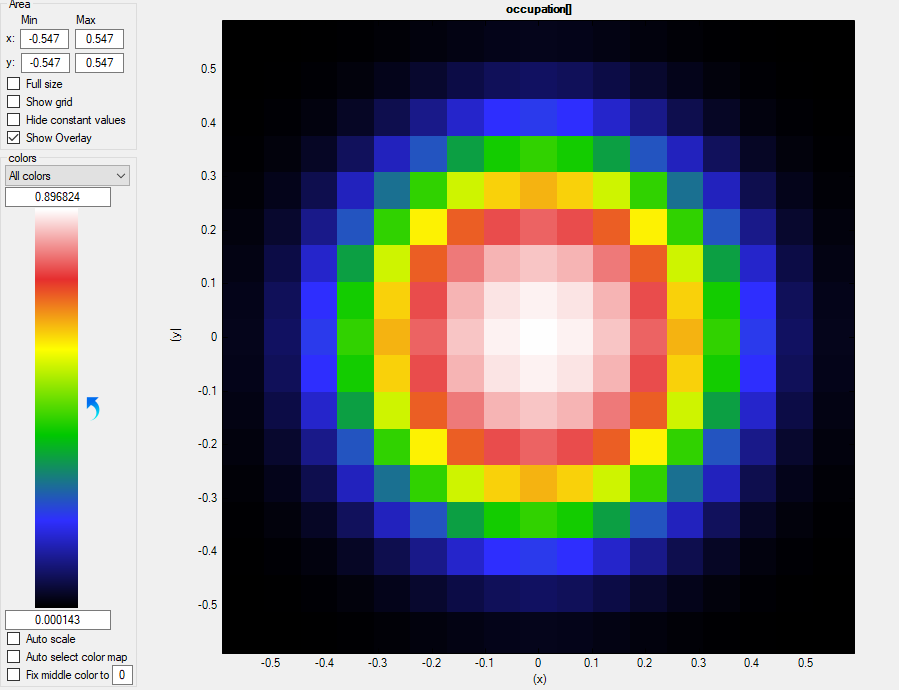
Figure 2.4.315 Occupation of the first (m=1) bound states as a function of
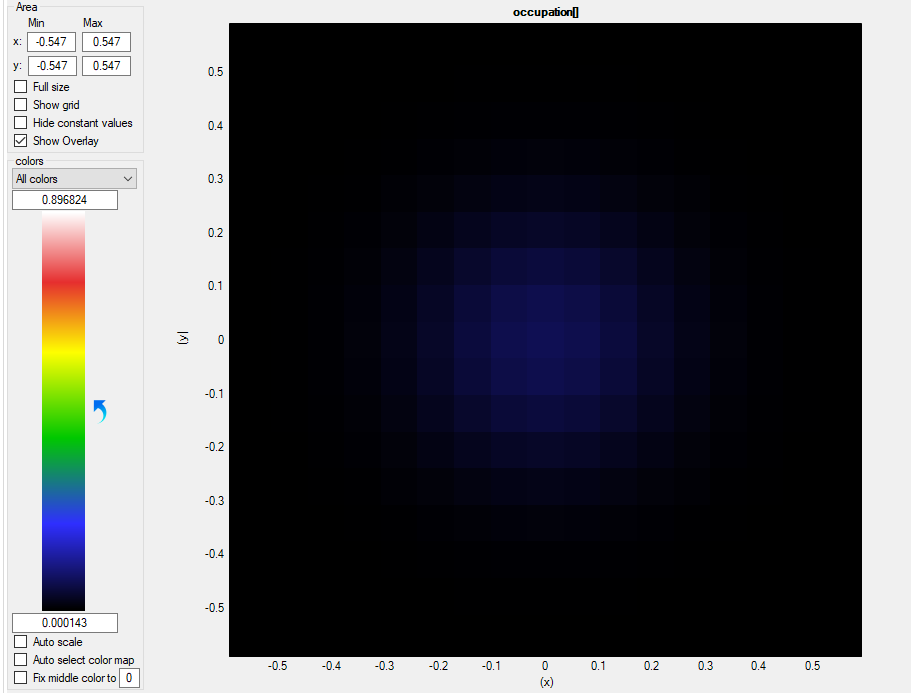
Figure 2.4.316 Occupation of the second (m=2) bound states as a function of
The autoscale mode in nextnanomat is set off here. We clearly see that the first state is well occupied, whereas for the second state is not (precisely speaking
The absorption coefficient for TE ($ENERGY_RESOLUTION=0.5meV.
For single-band models the peak becomes very sharp unless one introduces phenomenological broadening function such as Lorentzian.
In k.p calculation, in contrast, peaks gets broadened because the transition energies, \Optics\energy_disp_~.dat for states m=1 and 2 (not shown).
In intersubband transitions the transition energies can be concave downward in k|| space, i.e.,

Figure 2.4.317 Absorption coefficient in \Optics\absorption_~.dat as a function of photon energy, for TE and TM. Black arrow points the energy separation
The optical transitions between conduction band states (intersubband transitions) in response to TE-polarized light is only allowed when eigenstates have finite spinor components in valence bands. In the present case its large band gap and small confinement leads to small band-mixing, rendering TE absorption spectrum orders of magnitude smaller than TM polarization (Figure 2.4.317).
As seen in the output \Quantum\spinor_composition_~.dat, eigenstates contain approximately 98% contribution from conduction band and 2% from valence band.
InAs/AlSb single QW - small band gap & large confinement
In the second example QWIP_singleQW_InAs_AlSb_nnp.in, single quantum well is narrower and the band gap is smaller than the first example.
The small band gap and large confinement of the wave function (Figure 2.4.318) leads to large band mixing.
In fact, the output \Quantum\spinor_composition_~.dat shows that the ground states in Figure Figure 2.4.318 consists of 80.7% of conduction band and 19.3% of valence band contribution.

Figure 2.4.318 Confined states at \Quantum\probabilities_shift_optical_active) in a narrower and deeper quantum well. The blue line marks the electron Fermi energy (0eV).
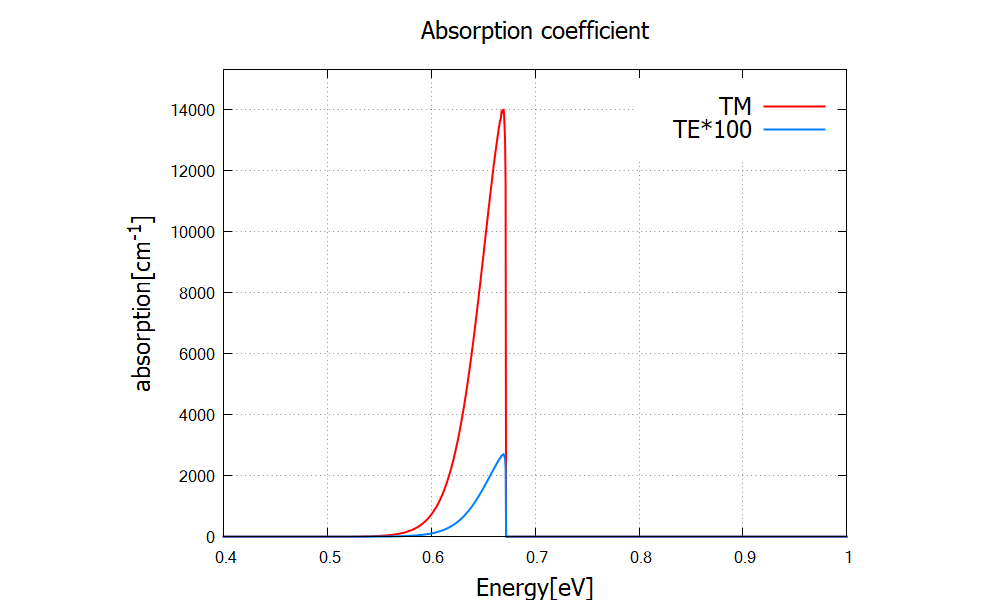
Figure 2.4.319 Absorption spectrum for TE and TM. TE absorption becomes relevant compared to Figure 2.4.317 because of the large band-mixing. Note that TE spectrum here is multiplied by a factor of 100, instead of 1000 in Figure 2.4.317.
Periodic case
In the third example QWIP_Gunapala_JAP_1991_nnp.in, we set the bias to zero and impose the periodic boundary condition.
The GaAs/Albandedges.dat and wave functions \Quantum\probabilities_shift.dat are shown in Figure 2.4.320.
We have continuum states above the barriers as well as bound states in the superlattice (miniband).
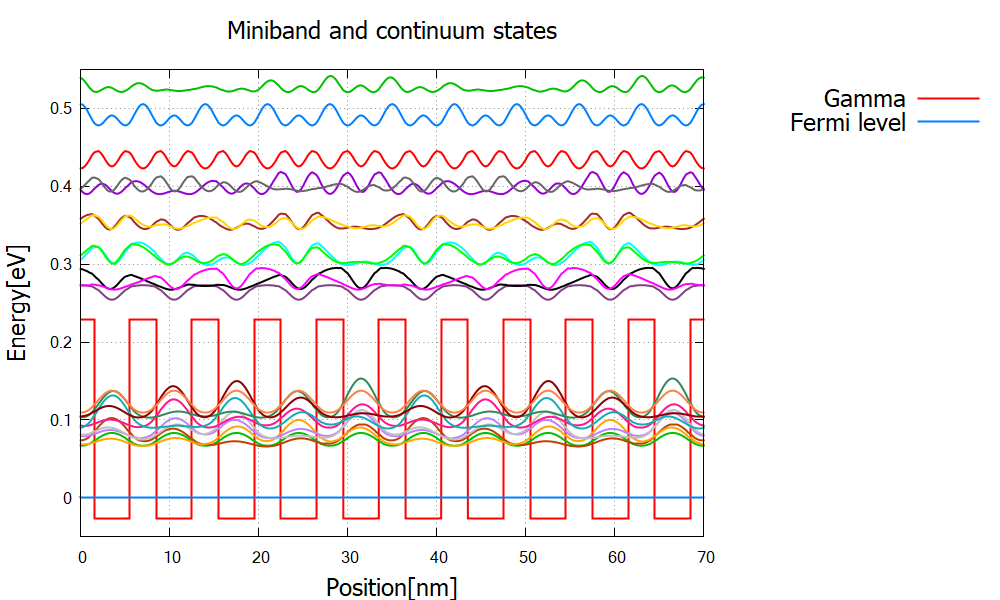
Figure 2.4.320 Gamma band profile and probability distribution of the bound miniband states and continuum states above the top of the barriers.
The absorption coefficient is exported to \Optics\absorption.
The indices in the filename *_kp8_TE_m_n.dat refer to the transition from state m to state n.
The files without indices contain the total absorption spectrum (sum over all transitions).
The total absorption spectrum for TE and TM polarization looks like this:

Figure 2.4.321 Absorption spectrum for TE (
The peak positions do not depend on polarization, while the peak height is much larger for TM polarization compared to the one for TE. Looking at the absorption spectrum for each transition, we identify which transition contributes to which peak (Figure 2.4.322).
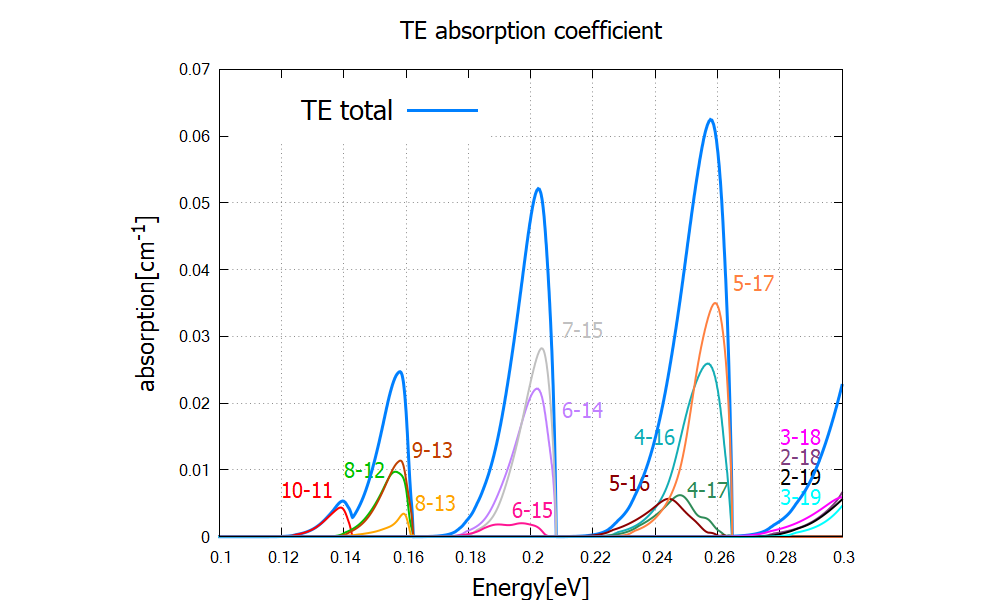
Figure 2.4.322 Contributions from different transitions to the total TE absorption spectrum.
Let us look at the eigenvalue and occupation of each state to confirm this result.
The eigenvalues of the bound- and continuum states are written in the output \Quantum\probabilities_shift.dat or \Quantum\energy_spectrum.
Note
quantum{ } uses spin-resolved index for the eigenstates, so there are 80 states in total.
In optics{ }, however, two spin-degenerate states are summed up and there are only 40 states.
This number (1 to 40) is used in the \Optics output filenames.
For the consistency, we use the latter notation throughout. (To do: examine the specifier spin_degeneracy)
Based on the indices in Figure 2.4.322, we identify the first four peaks to the following four different transitions (Figure 2.4.323). We have confirmed that the peak energies in Figure 2.4.322 are consistent to the energy separation of the corresponding states.
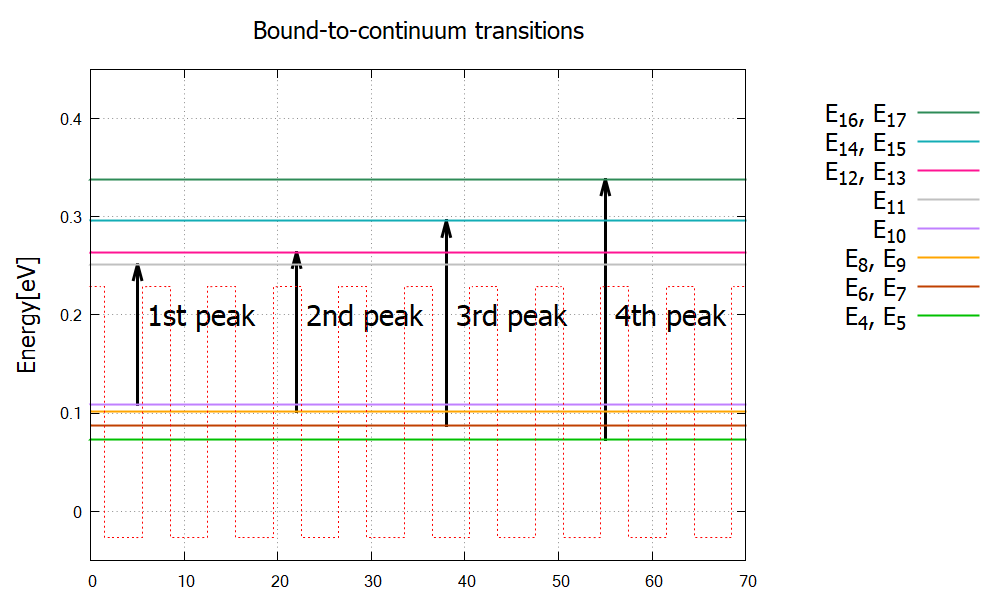
Figure 2.4.323 Eigenenergies of relevant bound- and continuum states.
Many other transitions have little contribution due to the shape of the wave functions and/or occupation of the states.
When we calculate for wider energy range, i.e. increase the parameter $ENERGY_MAX, there will be many more peaks that are attributed to higher energy transitions.
Lastly we check the occupation (Fermi-Dirac distribution) \Optics\eigenvaluespectrum (Figure 2.4.324), occupation at k||=0 of
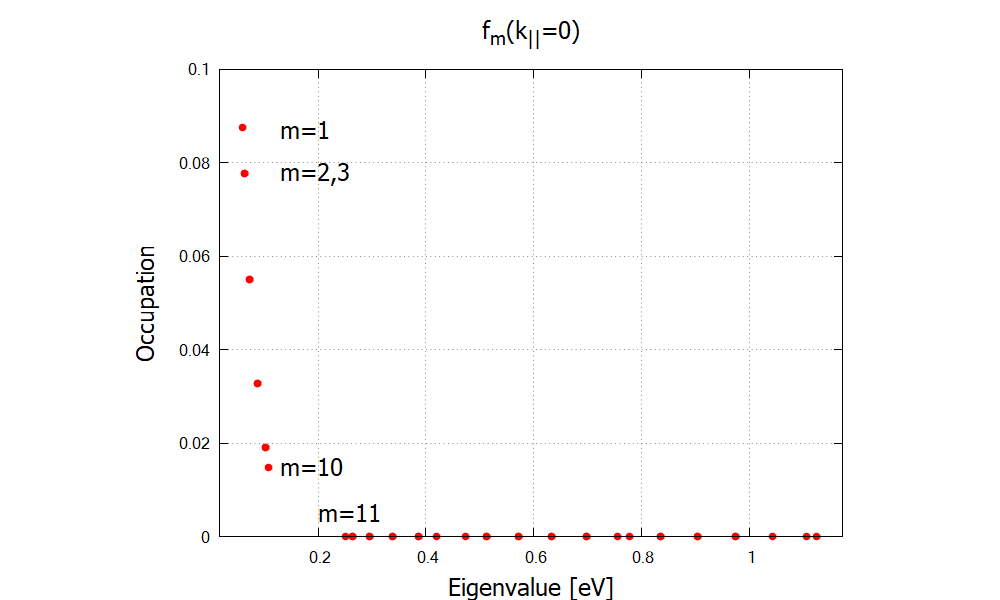
Figure 2.4.324 Occupation of eigenstates showing a noticeable difference for bound (m=1-10) and continuum (m=11,…) states.
1D tutorial for interband transitions: Frankenberger
Input files
AlGaAs_QW_Frankenberger_Simple_nnp.in
AlGaAs_QW_Frankenberger_Simple_nnp_fast.in
AlGaAs_QW_Frankenberger_Doping_schottky07_nnp.in
AlGaAs_QW_Frankenberger_Doping_schottky07_nnp_fast.in
These files are located in the sample files folder.
The fast examples reduce the computation load by limiting exact solution only to force_k0_subspace; see quantum{ } and optics{ } documentations).
Optical absorption and interband transitions
In the input file AlGaAs_QW_Frankenberger_Simple_nnp.in, we consider a single quantum well structure:
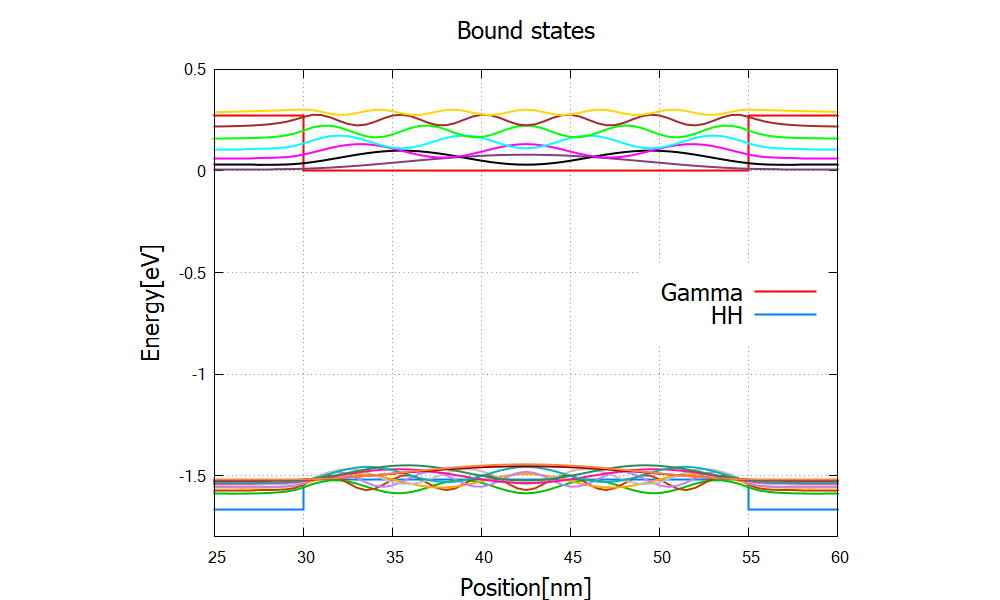
Figure 2.4.325 The conduction band edge profile (bandedges.dat) and wave functions of the bound states (\Quantum\probabilities_shift).
The program solves the 8-band k.p model coupled to the Poisson equation to find the eigenstates and compute the absorption coefficient.
Figure Figure 2.4.326 shows the absorption spectrum for circularly polarized light (
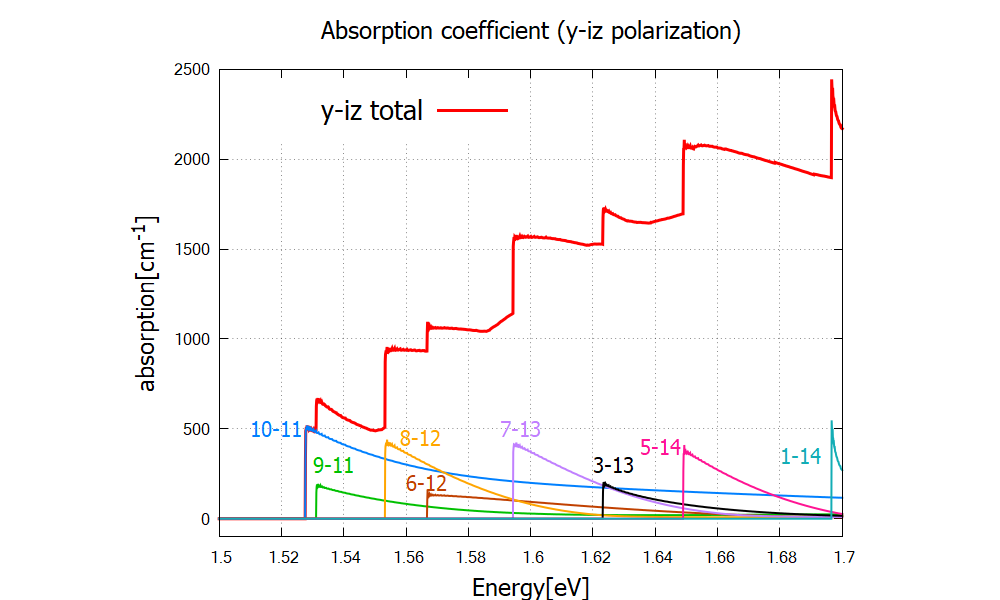
Figure 2.4.326 Absorption coefficient of circularly polarized lights. Numbers “m-n” denote each transition
The steps of this absorption spectrum are associated with the following interband transitions:

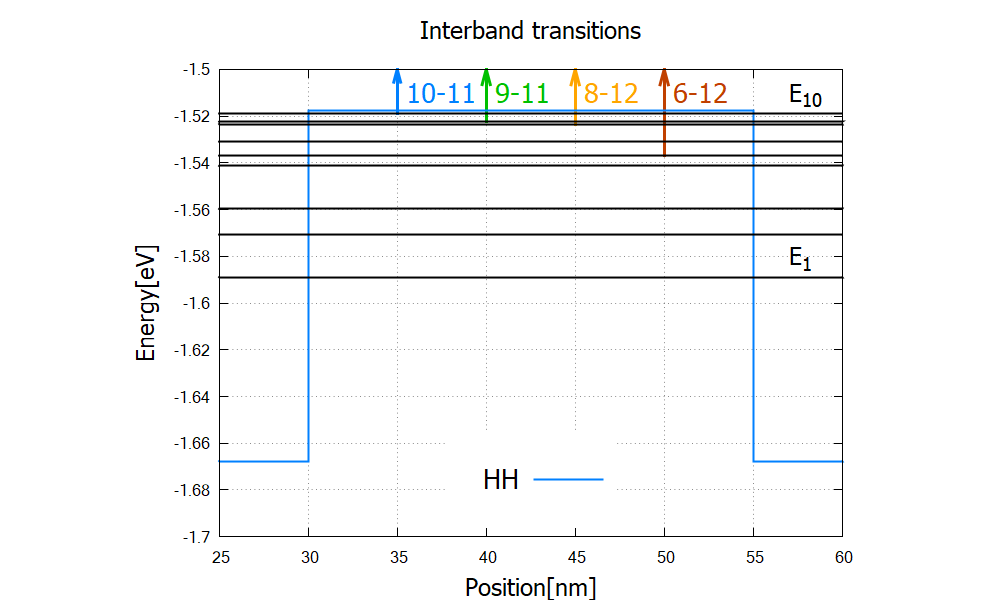
Figure 2.4.327 Eigenvalues (black) and transitions from valence-band to conduction band bound states (arrows) which are responsible for the first four steps in Figure 2.4.326.
Here spin-degenerate states are counted as one state (eigenstate numbering in optics{ }).
Note
In the end of the log file, you find the message “Integration reliable up to —eV”.
This tells you up to which energy the absorption spectrum is reliable.
Since we only consider the vicinity of the origin
where optics{ region{ k_integration{} } } with parameters interband=yes and intraband=no in optics{ } flag.
Doping and Schottkey barrier
In the second input file AlGaAs_QW_Frankenberger_Doping_schottky07_nnp.in, we consider the following structure:

Figure 2.4.328 The band structure and eigen functions used for optics calculation. The Fermi level is at 0eV.
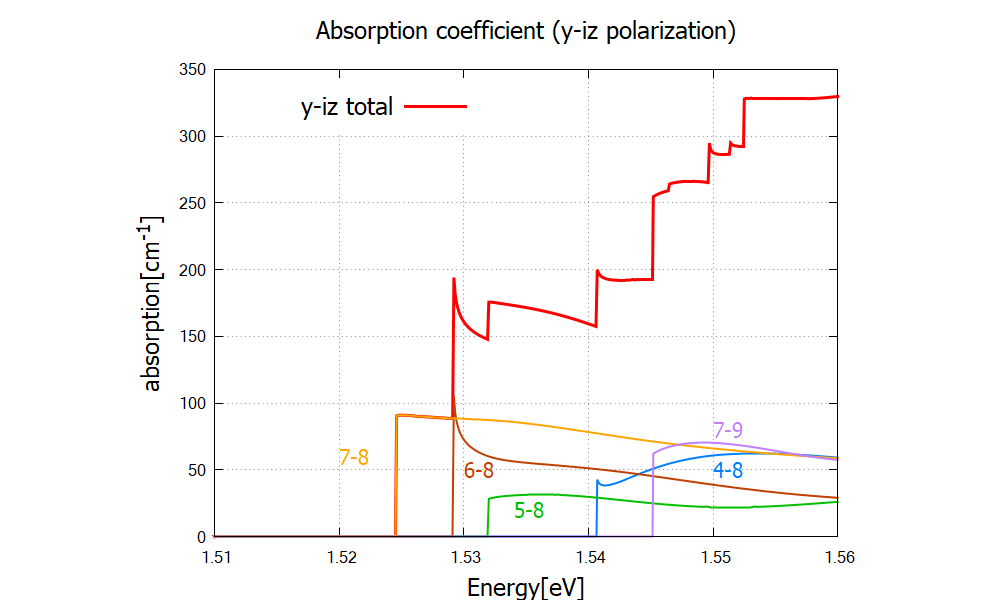
Figure 2.4.329 Absorption coefficient of circularly polarized lights. Numbers “m-n” denote each transition
Figure 2.4.330 compares the results for different settings for occupation optics{ occupation_ignore=yes }, valence bands and conduction bands are considered to be fully occupied and fully empty, respectively.
When the actual occupation of eigenstates are taken into account, in contrast, optical transitions to conduction band states just above the Fermi energy are prohibited because of the thermal distribution of electrons.
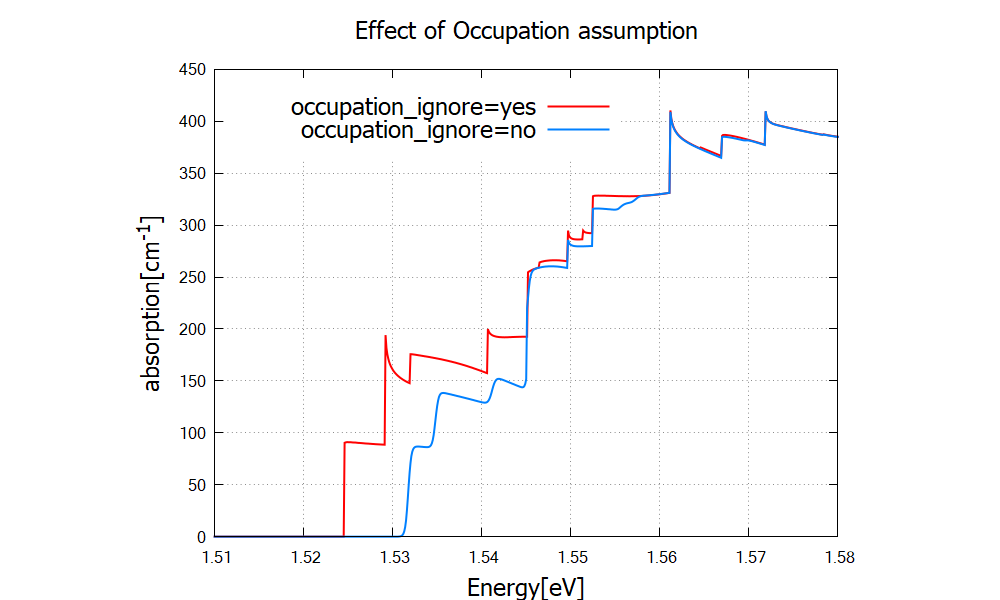
Figure 2.4.330 Absorption coefficient for different settings of occupation.
The red curve is identical to the total absorption spectrum in Figure 2.4.329.
When occupation_ignore=no, absorption of low energy photons is suppressed due to the occupation of the lowest conduction band states (also see Figure 2.4.328).
Last update: nnnn/nn/nn