nextnano3 - Tutorial
next generation 3D nano device simulator
1D Tutorial
Growth of layers on strained (or stressed) substrates (biaxial and uniaxial)
Authors:
Stefan Birner, Michael
Povolotskyi
-> 1D_GaAs_biaxial_on_InAs001.in
-> 1D_InAs_on_biaxially_strainedGaAs001.in
-> 1D_InAs_on_uniaxially_stressedGaAs001.in
-> 1D_InAs_on_uniaxially_stressedGaAs001_input_stress.in
-> 1D_InAs_on_biaxially_stressedGaAs001.in
-> 1D_InAs_on_biaxially_stressedGaAs001_input_stress.in
These input files are included in the latest version.
Growth of layers on strained (or stressed) substrates (biaxial and uniaxial)
In this tutorial we show how to input a fixed strain tensor for a
semiconductor starting layer in addition to its bulk lattice constants.
All other semiconductor layers that are grown on top are pseudomorphically
strained with respect to the strained substrate layer.
In other words, the strain tensor of one specific layer is kept fixed whereas in
all other layers the elastic energy is going to be minimized.
Material parameters of GaAs and InAs
Lattice constants
GaAs: a = 0.565325 nm
InAs: a = 0.60583 nm
Elastic constants
GaAs: c11 = 122.1 GPa c12 =
56.6 GPa
InAs: c11 = 83.29 GPa c12 = 45.26 GPa
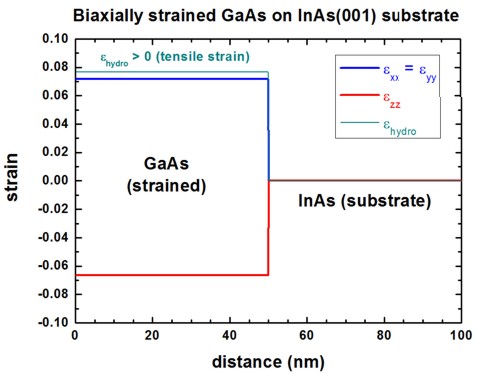
a) Biaxially strained GaAs on InAs(001) substrate
-> 1D_GaAs_biaxial_on_InAs001.in
If one assumes that GaAs is grown pseudomorphically with respect to an
unstrained InAs(001) substrate along the z direction, then the following strain
tensor components are obtained:
exx = eyy = e|| = ( asubstrate
- alayer ) / alayer = 0.071649051
ezz = e_|_ = - D001 e||
= - 2 (c12/c11) e||
= - 0.066426474
ehydro = Tr(e) = exx + eyy + ezz
= 0.076871628
Here, GaAs is biaxially strained and the overall strain is tensile (i.e. the
hydrostatic strain ( Tr(eij) ) is positive) because GaAs has a
smaller lattice constant than InAs.
b) InAs on biaxially strained GaAs(001) substrate
-> 1D_InAs_on_biaxially_strainedGaAs001.in
We now grow InAs pseudomorphically on a strained GaAs substrate
where the GaAs substrate has the following strain tensor components:
$strain-minimization-model
...
input-substrate-strain = yes
! 'yes' = read in strain tensor
components of substrate
strain-epsilon-substrate-xx = 0.071649051d0
!
strain-epsilon-substrate-yy = 0.071649051d0
!
strain-epsilon-substrate-zz = -0.066426474d0 !
strain-epsilon-substrate-xy = 0d0
!
strain-epsilon-substrate-xz = 0d0
!
strain-epsilon-substrate-yz = 0d0
!
If one minimizes the elastic energy with respect to the strained
GaAs substrate, then InAs is calculated to be unstrained, as one would expect.
Note that the GaAs substrate's lattice constants are kept fixed.
The same result would be obtained if strain-epsilon-substrate-zz takes an
arbitrary value, as only the in-plane strain tensor components e||
are relevant.
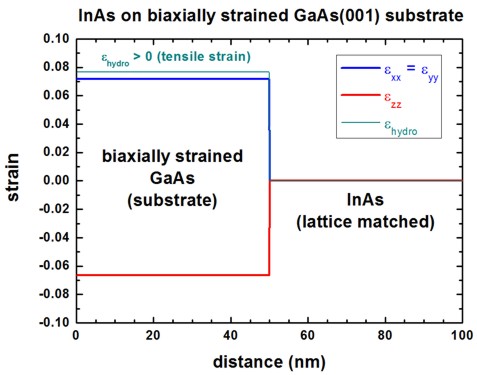
Obviously, the substrate can have any arbitrary strain tensor components,
e.g. hydrostatic, biaxial, uniaxial or shear strain.
c) InAs on uniaxially and biaxially strained GaAs(001) substrate
Again, the material system is an InAs layer grown on a GaAs(001) substrate
that itself is subject to a variable uniaxial or biaxial stress.
We first apply a tensile uniaxial stress of 1 GPa ( = 10 kbar) on the GaAs
substrate followed by a tensile biaxial stress of 1 GPa ( = 10 kbar).
Since nextnano≥ accepts as inputs the strain tensor components of the
substrate (and not the stress), we first have to calculate these components
based on uniaxial and biaxial stresses of 1 GPa.
- Tensile, uniaxial stress of 1 GPa: (sigmaxx = 1 GPa,
all other stress tensor components of sigma are zero.)
a) Reading in the strain tensor
-> 1D_InAs_on_uniaxially_stressedGaAs001.in
sigmai = Eij . epsilonj
(i,j = 1...6) (matrix-vector
notation of Hooke's law, Voigt notation, Eij is the elasticity
matrix)
In this particular example (uniaxial for zinblende) it holds for the three
unknows exx, eyy, ezz:
(Note that all shear components are zero for this case.)
sigmax = sigmaxx = c11 * epsilon1
+ c12 * epsilon2 + c12 * epsilon3
=
= c11 * exx
+ c12 * eyy
+ c12 * ezz = 1 GPa
sigmay = sigmayy = c12 * epsilon1
+ c11 * epsilon2 + c12 * epsilon3
=
= c12 * exx
+ c11 * eyy
+ c12 * ezz = 0
sigmaz = sigmazz = c12 * epsilon1
+ c12 * epsilon2 + c11 * epsilon3
=
= c12 * exx
+ c12 * eyy
+ c11 * ezz = 0
These are three equations with three unknowns whereas due to symmetry
arguments, it additionally holds: eyy = ezz
==> exx = sigmaxx / [c11
- 2 c122 / (c11 + c12)
] = 0.011594748
==> eyy = ezz = - c12
/ (c11 + c12) * exx = -0.003672427
Thus the following strain tensor corresponds to a strained GaAs substrate
with a uniaxial stress along the x direction of 1 GPa:
input-substrate-strain = yes
! 'yes' = read in strain tensor
components of substrate
strain-epsilon-substrate-xx = 0.011594748d0
!
strain-epsilon-substrate-yy = -0.003672427d0
!
strain-epsilon-substrate-zz =
-0.003672427d0 !
strain-epsilon-substrate-xy =
0d0
!
strain-epsilon-substrate-xz =
0d0
!
strain-epsilon-substrate-yz =
0d0
!
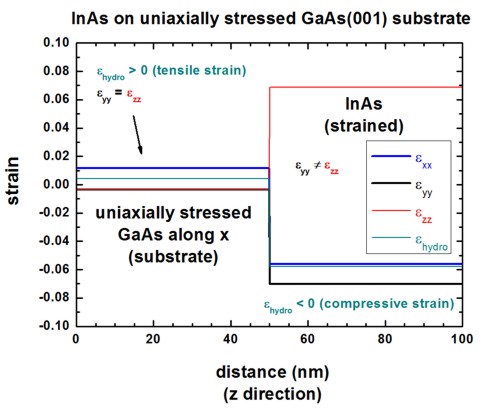
Thus the InAs has the following strain tensor components:
exx = -0.0560392
eyy = -0.0702856
ezz = 0.0686452
This corresponds to a compressive, hydrostatic strain
in InAs of ehydro
= -0.0576795.
-> 1D_InAs_on_uniaxially_stressedGaAs001_input_stress.in
input-substrate-stress = yes
! 'yes' =
stress-sigma-substrate-xx = 1d9
! [Pa] !
stress-sigma-substrate-yy = 0d0 !
stress-sigma-substrate-zz =
0d0 !
stress-sigma-substrate-xy =
0d0
!
stress-sigma-substrate-xz =
0d0
!
stress-sigma-substrate-yz =
0d0
!
- Tensile, biaxial stress of 1 GPa: (sigmaxx = sigmayy
= sigma|| = 1 GPa = 10 kbar, all other stress tensor components
of sigma are zero.)
-> 1D_InAs_on_biaxially_stressedGaAs001.in
The formulas (similar as above) lead to the following analytical equations:
==> exx = eyy = e|| = sigma||
c11 / (2 c122 -
c112 - c11c12)
= 0.007922321
==> ezz = e_|_ = - D001
e|| = - 2 (c12/c11)
e|| = -0.007344854
Thus the following strain tensor corresponds to a strained GaAs substrate
with a biaxial stress along the x and y directions of 1 GPa:
input-substrate-strain = yes
! 'yes' = read in strain tensor
components of substrate
strain-epsilon-substrate-xx = 0.007922321d0
!
strain-epsilon-substrate-yy = 0.007922321d0
!
strain-epsilon-substrate-zz =
-0.007344854d0 !
strain-epsilon-substrate-xy =
0d0
!
strain-epsilon-substrate-xz =
0d0
!
strain-epsilon-substrate-yz =
0d0
!
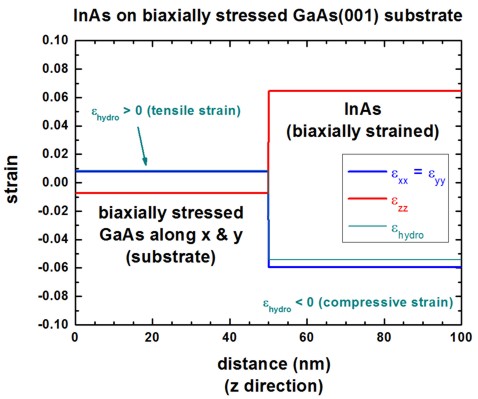
Thus the InAs has the following strain tensor components:
exx = -0.0594660
eyy = -0.0594660
ezz = 0.0646280
This corresponds to a compressive, hydrostatic strain in InAs of ehydro
= -0.0543041.
b) Reading in the stress tensor
-> 1D_InAs_on_biaxially_stressedGaAs001_input_stress.in
input-substrate-stress = yes
! 'yes' =
!
stress-sigma-substrate-xx = 1d9
! [Pa] sigmaxx = 1 GPa along the
x direction and with.
stress-sigma-substrate-yy = 1d9 !
[Pa]
stress-sigma-substrate-zz =
0d0 ! [Pa]
stress-sigma-substrate-xy =
0d0
! [Pa]
stress-sigma-substrate-xz =
0d0
! [Pa]
stress-sigma-substrate-yz =
0d0
! [Pa]
The features presented in this tutorial can be used to model stresses that
often occur in the case of thermal expansion mismatches for III-V films grown on
sapphire or silicon substrates.
The selective growth on pre-patterned mesas where local stress/strain variations
obviously play a crucial role in the resulting electronic/optical properties is
another possible application.
|