nextnano3 - Tutorial
next generation 3D nano device simulator
3D Tutorial
Artificial quantum dot crystal - Superlattice dispersion (minibands)
Author:
Stefan Birner
If you want to obtain the input files that are used within this tutorial, please
check if you can find them in the installation directory.
If you cannot find them, please submit a
Support Ticket.
-> 3DSuperlatticeDispersion_ArtificialQDCrystal_cubic.in
-> 3DSuperlatticeDispersion_ArtificialQDCrystal_tetragonal_025nmgrid_PRB.in
Artificial quantum dot crystal - Superlattice dispersion (minibands) of
cubic QDs
-> 3DSuperlatticeDispersion_ArtificialQDCrystal_cubic.in
This tutorial is based on the following paper:
[Balandin]
Miniband formation in a quantum dot crystal
O.L. Lazarenkova, A.A. Balandin
Journal of Applied Physics 89, 5509 (2001)
We calculate the superlattice energy dispersion for an artificial crystal
consisting of cubic QDs.
- The QD has a cubic shape with Lx = Ly = Lz
= 6.5 nm.
- The QDs are separated by a distance of Hx = Hy = Hz
= 1.5 nm.
- superlattice period: dx = dy = dz = 8
nm (di = Li + Hi)
- We only model one QD and assume periodic boundary conditions along the
x, y and z direction.
- We solve the single-band Schrödinger equation for the valence band only
(heavy hole).
- The valence band offset is assumed to be VBO = 0.45 eV,
i.e. the valence band edge of the QD is at +0.45 eV, the valence band edge
of the barrier is at 0 eV.
- QD material: Ge, barrier material: Si
- effective heavy hole masses (isotropic):
QD: 0.28 m0 (Ge), barrier: 0.49 m0 (Si)
- grid spacing: 0.5 nm in x, y and z direction, i.e. 16 grid points in
each direction.
size of Schrödinger matrix to be solved: 16 * 16 * 16 = 4096
(60 eigenvalues are calculated)
Required superlattice options
$numeric-control
...
!superlattice-option = 100-only ! for
dispersion along [100] direction in superlattice Brillouin zone, i.e. from Gamma
to X
superlattice-option = 110-only !
!superlattice-option = 111-only !
$quantum-model-holes
...
model-name
= effective-mass !
number-of-eigenvalues-per-band = 60
! how many eigenenergies have to be calculated in each band
boundary-condition-100 =
periodic !
boundary-condition-010 =
periodic !
boundary-condition-001 =
periodic !
!num-ks-100
= 1
!
num-ks-100
= 11
!
!num-ks-010
= 1
!
num-ks-010
= 11
!
!num-ks-001
= 1
!
num-ks-001
= 11
!
Dispersion relation along [100] direction
superlattice-option = 100-only !
for dispersion along [100] direction in superlattice Brillouin zone, i.e.
from Gamma to X
The following figure shows the calculated dispersion relation along the [100]
direction.
The figure agrees very well with Fig. 2(a) of the paper by [Balandin]
in the energy region where the confinement inside the QD is strong.
For the higher lying states inside the QD and above the QD, our results differ
because we use the correct 3D QD confinement potential whereas [Balandin]
approximated the potential landscape with an analytical ansatz that
allows for the separation of the x, y and z variables. (This ansatz is only
justified for states confined deep inside the QD.)
The right part of the figure shows schematically the valence band edge of the QD
with the energy levels of the single, uncoupled QD.
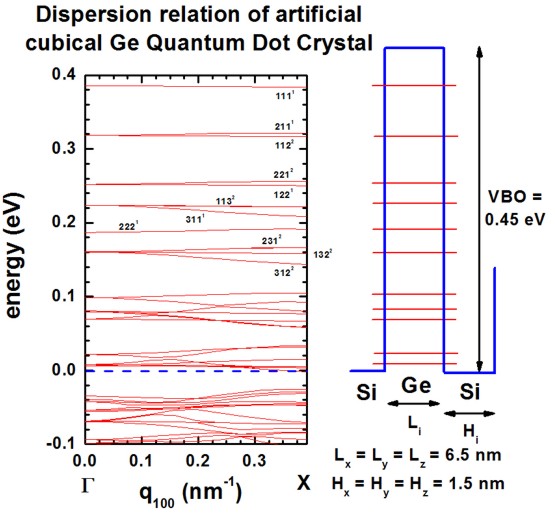
In the figure, the eigenstates are labeled with the quantum numbers nxnynz,
e.g. 111.
The superscript refers to their degeneracy.
At KSL=0, the degeneracy is higher than at nonzero KSL
vectors where the symmetry in the Brillouin zone is lower.
(The superlattice vector "KSL" is often denoted as "q".)
Dispersion relation along [110] and [111] direction
superlattice-option = 110-only !
for dispersion along [110] direction in superlattice Brillouin zone, i.e.
from Gamma to K
!superlattice-option = 111-only !
The following figure shows the calculated dispersion relations along the [110]
and [111] directions.
The agreement to Fig. 2(b) and 2(c) of [Balandin] is again very
good for the states that lie deep inside the QD (see also comments above).
Note that the eigenstates along the [111] direction show a higher degree of
degeneracy throughout the superlattice Brillouin zone as compared to [100] and
[110].
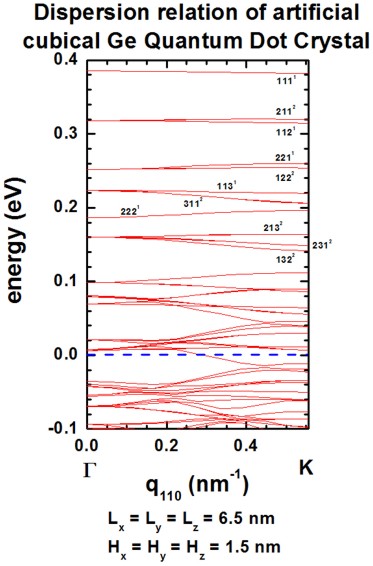 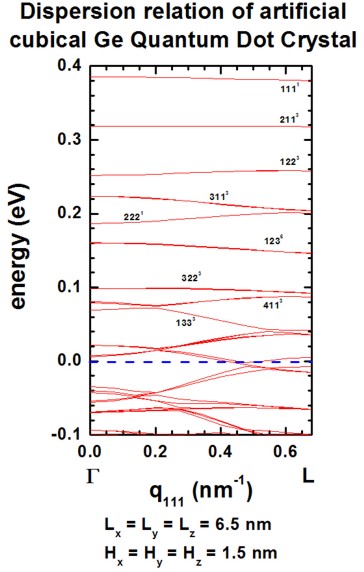
Both, the QD itself and the QD superlattice have the same cubic symmetry in this
example. Thus the degeneracy of the 123 (incl. permutations) energy band is
sixfold throughout the Brillouin zone along the [111] directions (as shown in
right figure).
Output
The output that was plotted in these figures can be found in this file:
Schroedinger_1band/sg_dispSL3D_hl_qc001_sg001_deg001_evmin001_evmax060.dat
This file contains information about the superlattice vector KSL
(in units of [pi/Li] and [1/Angstrom]), and the corresponding
eigenvalues.
norm[pi/L] norm[1/AA] k_x[pi/L_x] k_x[1/AA] k_y[pi/L_y] k_y[1/AA]
k_z[pi/L_z] k_z[1/AA] 1 2 3 ... 60
... ...
... ...
... ...
... ...
. . . ... .
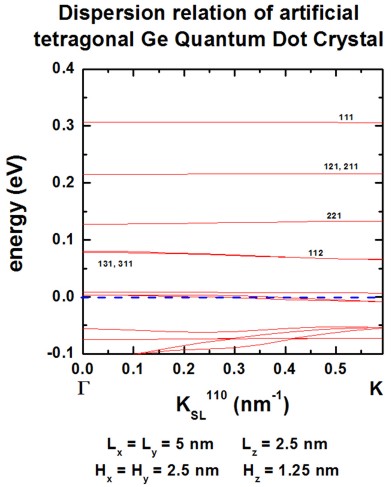
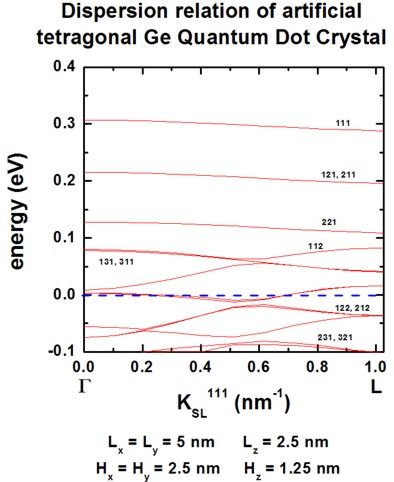
Artificial quantum dot crystal - Superlattice dispersion (minibands) of
tetragonal QDs
->
3DSuperlatticeDispersion_ArtificialQDCrystal_tetragonal_025nmgrid_PRB.in
See also the following paper for similar calculations, especially with respect
to comparing the numercial vs. the analytical (separation of variables) results.
[Balandin2]
Electron and phonon energy spectra in a three-dimensional regimented quantum
dot superlattice},
O.L. Lazarenkova, A.A. Balandin
Physical Review B 66, 245319 (2002)
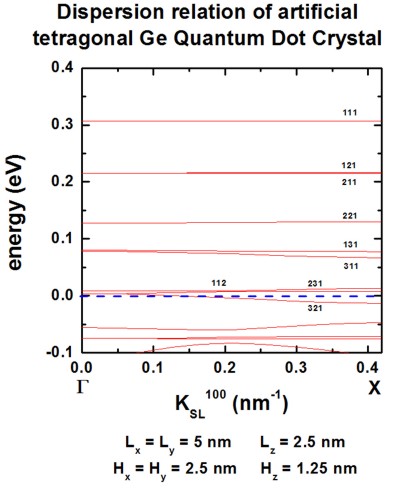
We calculate the superlattice energy dispersion for an artificial crystal
consisting of tetragonal QDs.
- The QD has an tetragonal shape with Lx = Ly = 5
nm and Lz = 2.5 nm.
- The QDs are separated by a distance of Hx = Hy
= 2.5 nm and Hz = 1.25 nm.
- superlattice period: dx = dy = 7.5 nm and dz
= 3.75 nm (di = Li + Hi)
- grid spacing: 0.25 nm in x, y and z direction, i.e. 30 grid
points in x and y direction, 15 grid points in z direction.
size of Schrödinger matrix to be solved: 30 * 30 * 15 = 13500
- All other assumptions are the same as for the above cubic QD example.
The following figures show the dispersion along the [100], [110] and [111]
directions.
All results are in very good agreement to Fig. 4 of [Balandin].
See also this tutorial for one-dimensional superlattices:
Dispersion in infinite superlattices: Minibands
|