k.p dispersion of an unstrained GaN QW embedded between strained AlGaN layers

Input files:

• 1DGaN_AlGaN_QW_k_zero_nnp.in

• 1DGaN_AlGaN_QW_k_parallel_nnp.in

• 1DGaN_AlGaN_QW_k_zero_10m10_nnp.in

• 1DGaN_AlGaN_QW_k_parallel_10m10_nnp.in

• 1DGaN_AlGaN_QW_k_parallel_10m10_whole_nnp.in

Scope:

In this tutorial we aim to reproduce results of [Park2000]. The material parameters are taken from [ParkChunag2000], except those listed in Table 1 of [Park2000].

[0001] growth direction

Calculation of electron and hole energies and wave functions for $k_{||}$ = 0

Input file: 1DGaN_AlGaN_QW_k_zero_nnp.in

The structure consists of a 3 nm unstrained $GaN$ quantum well, embedded between 8.4 nm strained $A{l}_{0.2}G{a}_{0.8}N$ barriers. The $AlGaN$ layers are strained with respect to the $GaN$ substrate. The $GaN$ quantum well is assumed to be unstrained.

The structure is modeled as a superlattice (or multi quantum well, MQW), i.e. we apply periodic boundary conditions to the Poisson equation.

The growth direction is along the hexagonal axis, i.e. along [0001].

Conduction and valence band profile

Figure 2.4.261 shows the conduction and valence (heavy hole, light hole and crystal-field split-off hole) band edges of our structure, including the effects of strain, piezo- and pyroelectricity. The ground state electron and the ground state heavy hole wave functions (${\mathrm{\Psi }}^2$) are shown. Due to the built-in piezo- and pyroelectric fields, the electron wave function are shifted to the right and the hole wave function to the left (Quantum Confined Stark Effect, QCSE)

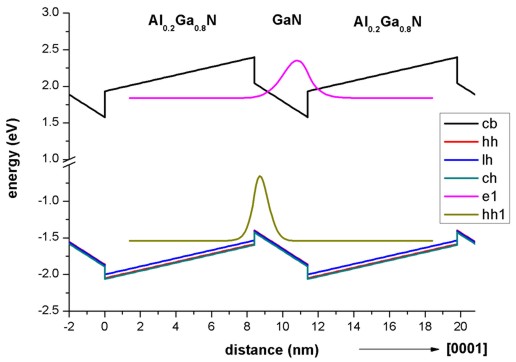
Figure 2.4.261 Calculated band edge profile.

Strain

The strain inside the $GaN$ quantum well layer is zero. The tensile strain in the $A{l}_{0.2}G{a}_{0.8}N$ barriers has been calculated to be

$$e_{xx}=e_{yy}=\frac{a_{\mathrm{substrate}}-a}{a}=0.486.$$

[Park2000] gives a value of 0.484.

The output of the strain tensor can be found in this file: strain\strain_crystal.dat

Piezoelectric polarization

The piezoelectric polarization for the [0001] growth direction is zero inside the GaN QW, because the strain is zero in the QW. In the $A{l}_{0.2}G{a}_{0.8}N$ barriers, the piezoelectric polarization has been calculated to be 0.0081 C/m² in agreement with Fig. 1(a) of [Park2000] for angle $\theta$ = 0. The resulting piezoelectric polarization

• at the $A{l}_{0.2}G{a}_{0.8}N/GaN$ interface -0.0081 C/m² and

• at the $GaN/A{l}_{0.2}G{a}_{0.8}N$ interface is 0.0081 C/m².

Pyroelectric polarization

The pyroelectric polarization for the [0001] growth direction is -0.029 C/m² inside the $GaN$ QW. In the $A{l}_{0.2}G{a}_{0.8}N$ barriers, the pyroelectric polarization has been calculated to be -0.0394 C/m². The resulting pyroelectric polarization

• at the $A{l}_{0.2}G{a}_{0.8}N/GaN$ interface is -0.0104 C/m² and

• at the $GaN/A{l}_{0.2}G{a}_{0.8}N$ interface is 0.0104 C/m².

These results are in excellent agreement with Fig. 1(a) of [Park2000] for angle $\theta$ = 0.

Poisson equation

Solving the Poisson equation with periodic boundary conditions (to mimic the superlattice) leads to the following electric fields: Inside the $GaN$ QW the electric field has been calculated to be -1.551 MV/cm. [Park2000] reports an electric field of -1.55 MV/cm inside the QW. The electric field in the $AlGaN$ barrier has been found to be 0.554 MV/cm.

The output of the electrostatic potential (units [V]) and the electric field (units [kV/cm]) can be found in these files:

• bias_00000\potential

• bias_00000\electric_filed.dat

Schrödinger equation

Figure 2.4.262 shows the electron and hole wave functions (${\mathrm{\Psi }}^2$) of the $GaN/AlGaN$ structure for $k_{||}$ = 0. The heavy and light hole wave functions are very similar in shape.

In agreement with [Park2000], we calculated the electron levels within the single-band effective mass approximation and the hole levels within the 6-band k.p approximation.

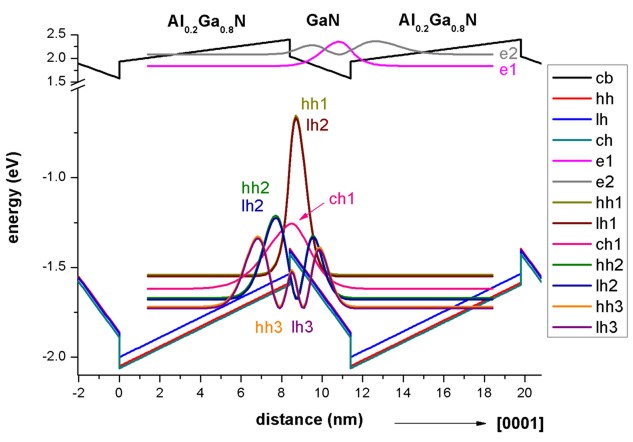
Figure 2.4.262 Calculated wave functions of lowest eigenstates.

$k_{||}$ dispersion: Calculation of the electron and hole energies and wave functions for $k_{||}\ne$ 0.

Input file: 1DGaN_AlGaN_QW_k_parallel_nnp.in

The grid has a spacing of 0.1 nm leading to a sparse matrix of dimension 1050 which has to be solved for each $k_{||}$ point for the eigenvalues (and wave functions).

We chose as input:

calculate_dispersion{
    num_points = 1849 # This corresponds to 1849 k|| points in the 2D (kx,ky) plane, i.e. (2 * 21 + 1) * (2 * 21 + 1) = 1849.
}

Due to symmetry arguments, we solved the Schrödinger equation only for the $k_{||}$ points along the line ($k_x$ > 0, $k_y$ = 0), i.e. we had to solve the Schrödinger equation 22 times (i.e. to calculate the eigenvalues of a 1050 x 1050 matrix 22 times).

The energy dispersion $E(k_{||})$ = $E(k_y,k_z)$ displayed in Figure 2.4.263 is contained in this folder: bias_00000\Quantum\Dispersion

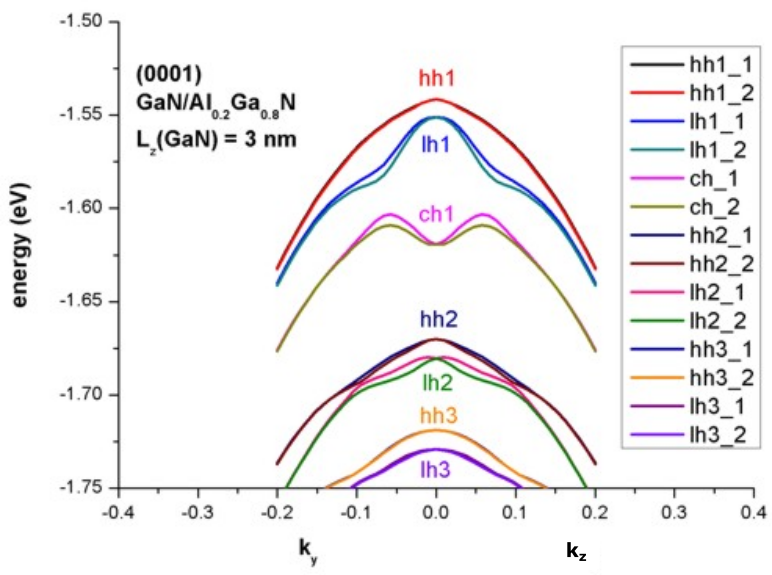
Figure 2.4.263 Calculated energy dispersion $E(k_{||})$ = $E(k_y,k_z)$.

Because our quantum well is not symmetric (due to the piezo- and pyroelectric fields), the eigenvalues for spin up and spin down are not degenerate anymore. They are only degenerate at $k_{||}$ = 0. This lifting of the so-called Kramer’s degeneracy in the in-plane dispersion relations is because of the field-induced asymmetry. In Fig. 3 (a) of [Park2000] only the spin-up eigenstates are plotted because the splitting of the Kramer’s degeneracy was assumed to be very small.

[10-10] growth direction (m-plane)

Input file: 1DGaN_AlGaN_QW_k_zero_10m10_nnp.in

If one grows the quantum well along the [10-10] growth direction, then the pyroelectric and piezoelectric fields along the [10-10] direction are zero. In this case, the quantum well (i.e. the conduction and valence band profile) is symmetric.

Figure 2.4.264 shows the electron and hole wave functions (${\psi }^2$) of the (10-10)-oriented $GaN/AlGaNQW$ for $k_{||}$ = 0. Obviously, the interband transition matrix elements (i.e. the probability for electron-hole transitions) are much larger than for the [0001] growth direction.

In agreement with [Park2000], we calculated the electron levels within the single-band effective mass approximation and the hole levels within the 6-band k.p approximation.

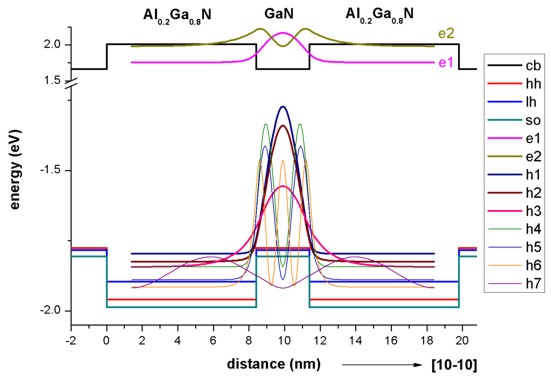
Figure 2.4.264 Calculated wave functions of lowest eigenstates.

$k_{||}$ dispersion: Calculation of the electron and hole energies and wave functions for $k_{||}\ne$ 0.

Input file: 1DGaN_AlGaN_QW_k_parallel_10m10_nnp.in

Due to the symmetry of the quantum well, we expect degenerate eigenvalues for the in-plane dispersion relation (Kramer’s degeneracy). Our results, depicted in Figure 2.4.265, compare well with Fig. 3(c) of [Park2000].

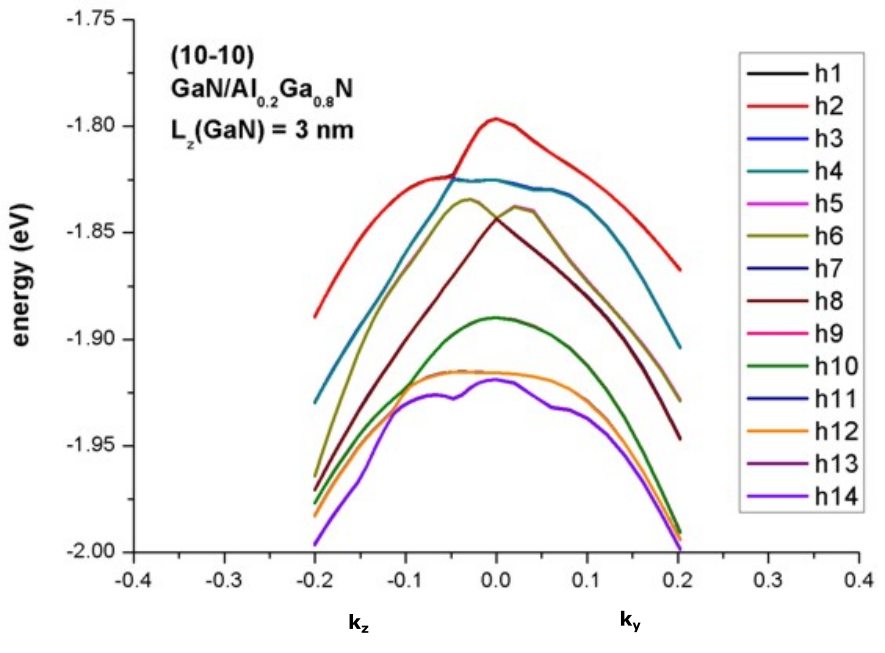
Figure 2.4.265 Calculated energy dispersion $E(k_{||})$ = $E(k_y,k_z)$.

---

Last update: nn/nn/nnnn